淀粉质
可以处理一些有关树上路径的问题,先看题 8️⃣
P3806
首先对于一个点 u u u v v v d i s ( v ) dis(v) d i s ( v ) v v v u u u
考虑开一个桶 u [ k ] u[k] u [ k ] d i s ( v ) = k dis(v) = k d i s ( v ) = k
那么不在同一个子树的两个点的贡献就好算了
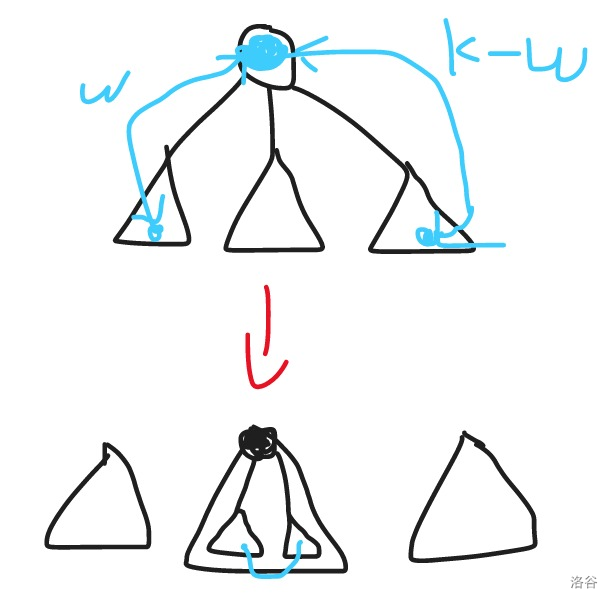
对于一个存在的 u [ w ] , w < = k u[w],w <= k u [ w ] , w < = k u [ k − w ] u[k-w] u [ k − w ]
对于在同一个子树内点的贡献,我们把 u u u
肯定是拆成的子树大小越均衡越好,所以每次节点 u u u
每次选取当前树的重心作为 u u u O ( n l o g n ) O(nlogn) O ( n l o g n )
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 #include <bits/stdc++.h> #define MAXN 10005 #define MAXK 10000005 #define ll long long #define cjb 1145141919 using namespace std;namespace F_star{ int cnte = 0 , head[MAXN]; struct edge { int to, nxt; ll dis; }e[MAXN << 1 ]; void adde (int u, int v, ll w) { e[++cnte].to = v; e[cnte].dis = w; e[cnte].nxt = head[u]; head[u] = cnte; } }using namespace F_star; struct query { int k, ans; }que[105 ]; int n,m;int siz[MAXN];int root, sixz, sum;ll dis[MAXN]; bool vis[MAXN];bool t[MAXK+5 ];void get_zx (int u) int msiz = 0 ; siz[u] = 1 ; vis[u] = true ; for (int i = head[u]; i; i = e[i].nxt) { int v = e[i].to; if (vis[v]) continue ; get_zx (v); siz[u] += siz[v]; msiz = max (msiz, siz[v]); } msiz = max (msiz, sum - siz[u]); if (msiz < sixz) {sixz = msiz; root = u;} vis[u] = false ; } ll sta1[MAXN], top1; ll sta2[MAXN], top2; int debug;void get_dis (int u) if (dis[u] > MAXK) return ; vis[u] = true ; sta1[++top1] = dis[u]; for (int i = head[u]; i; i = e[i].nxt) { int v = e[i].to; if (vis[v]) continue ; dis[v] = dis[u] + e[i].dis; get_dis (v); } vis[u] = false ; } void get_ans (int u) t[0 ] = 1 ; top2 = 0 ; vis[u] = true ; for (int i = head[u]; i; i = e[i].nxt) { int v = e[i].to; if (vis[v]) continue ; top1 = 0 ; dis[v] = e[i].dis; get_dis (v); for (int j = 1 ; j <= top1; j++) { for (int k = 1 ; k <= m; k++) { if (sta1[j] <= que[k].k) que[k].ans |= t[que[k].k - sta1[j]]; } } for (int j = 1 ; j <= top1; j++) sta2[++top2] = sta1[j], t[sta1[j]] = 1 ; } for (int i = 1 ; i <= top2; i++) t[sta2[i]] = 0 ; vis[u] = false ; } void solve (int u) get_ans (u); vis[u] = true ; for (int i = head[u]; i; i = e[i].nxt) { int v = e[i].to; if (vis[v]) continue ; sum = siz[v]; sixz = cjb; get_zx (v); solve (root); } } int main () scanf ("%d%d" ,&n, &m); for (int i = 1 ; i < n; i++) { int u, v, w; scanf ("%d%d%d" ,&u,&v,&w); adde (u, v, w); adde (v, u, w); } for (int i = 1 ; i <= m; i++) scanf ("%d" ,&que[i].k); sum = n; sixz = cjb; get_zx (1 ); solve (root); for (int i = 1 ; i <= m; i++) printf (que[i].ans ? "AYE\n" : "NAY\n" ); return 0 ; }
P4178 Tree
经典题
给定一个 n n n k k k
和板子题相比,询问从是否存在变为了查询点对数量,而且不再等于而是小于等于
小于等于的话,我们对桶求一个前缀和,就可以做到 O ( 1 ) O(1) O ( 1 )
发现加贡献实际上是单点修改,查询是区间查询,使用数据结构维护桶即可。
时间复杂度 O ( n l o g 2 n ) O(nlog^2n) O ( n l o g 2 n )
P2634 国家集训队 聪聪可可
给定一个 n n n 3 3 3
处理权值是 % 3 \% \ 3 % 3