树基础 - Veibae CN

🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳🌳

🌳相关

定义

森林，父亲，祖先，深度，二叉树，满二叉树

遍历

先序遍历

根 $\rightarrow$ 左 $\rightarrow$ 右

void prebl(int now)
{
    printf("%d ",now)
    prebl(ls(now));
    prebl(rs(now));
}

中序遍历

左 $\rightarrow$ 根 $\rightarrow$ 右

void midbl(int now)
{
    printf("%d ",now)  
    midbl(ls(now));
    midbl(rs(now));
}

后序遍历

左 $\rightarrow$ 右 $\rightarrow$ 根

void nxtbl(int now)
{
    nxtbl(ls(now));
    nxtbl(rs(now));
    printf("%d ",now)
}

树的直径

树上任意两个点之间最长的简单路径

两次DFS

先从任意一个节点 $u$ 出发，找到距离它最远的 $v$

再找到距离 $v$ 最远的 $z$ ，那么 $(u, z)$ 就是树的一条直径

证明

当存在负边权时，第一次dfs找到的 $v$ 不一定是直径的端点，所以这个方法不能处理负边

void dfs(int u, int fa)
{
    for(int i = head[u]; i; i = e[i].nxt)
    {
        int x = e[i].to;
        if(x == fa) continue;
        dis[x] = dis[u] + e[i].dis;
        if(dis[x] > dis[v]) v = x;
        dfs(x, u);
    }
}
int main()
{
    dfs(u, 0);
    dis[v] = 0;
    dfs(v, 0);
    printf("%d", dis[v]);
}

树形DP

int d1[MAXN], d2[MAXN], d;
void dfs(int u, int fa)
{
    d1[u] = d2[u] = 0;
   	for(int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].to; if(v == fa) continue;
        dfs(v, u);
        if(d1[v] + e[i].dis > d1[u])
        {
            d2[u] = d1[u];
            d1[u] = d1[v] + e[i].dis;
        }else if(d1[v] + e[i].dis > d2[u])
        	d2[u] = d1[v] + e[i].dis;
	}
    d = max(d, d1[u] + d2[u]);
}

时间复杂度都是 $O(n)$

P3629

k = 1时，只要把直径的两个端点连起来就行 $ans = (n-1)*2 - (d-1$ )

加一条边就会形成一个环，我们考虑第二条边形成的环与第一条边有没有重叠的部分

如果没有的话，直接加上就行，如果有的话，重叠部分就需要多走一次

如果我们第一次跑直径时，未来会重叠的边跑了一次，但是需要多跑一次

所以我们可以在第二次跑直径时，把重叠的边的权值设成 -1

$ans = (n - 1)*2 - (d_1-1) - (d_2 -1) = n*2 - d_1 - d_2$

树的重心

当以树上一点为根时，他的所有子树的结点数的最大值最小，那么这个点就是树的重心

也就是说重心把树相对平均的分为了几个部分

性质

一棵树最多有两个重心，如果有两个，这两个重心是相邻的
从重心到所有点的距离和是最小的
新加一个节点或删去一个节点，重心最多移动一条边
两棵树合并，新的重心在原来俩个重心的连线上

~~不会证，感性理解~~

我们选一个点为根dfs，记录每个节点下方的子树大小和点上方的子树大小

int zx, sizx = 1145141919;
int siz[MAXN], msiz[MAXN];//siz[u] u下方子树大小，msiz[u]u最大的子树大小
void dfs(int u, int fa)
{
    siz[u] = 1;
    for(int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].to; if(v == fa) continue;
		dfs(v, u);
        siz[u] += siz[v];
        msiz[u] = max(msiz[u], siz[v]);
    }
    msiz[u] = max(msiz[u], n - siz[u]);
    if(msiz[u] < sizx) sizx = msiz[u];
}
for(int i = 1; i <= n; i++)
{
    if(msiz[i] == sizx) 
	rt[++cnt] = i;
}

🌳 上问题

最近公共祖先LCA

倍增

void dfs(int u, int dad)
{
    dep[u] = dep[dad] + 1; fa[u][0] = dad;
    for(int i = 1; i <= l2g[dep[u]]; i++) fa[u][i] = fa[fa[u][i-1]][i-1];
    for(int i = head[u]; i; i = e[i].nxt) if(e[i].to != dad) dfs(e[i].to, u);
}

int lca(int x, int y)
{
    if(dep[x] < dep[y]) swap(x, y);
    while(dep[x] > dep[y]) x = fa[x][l2g[dep[x] - dep[y]] - 1];
    if(x == y) return x;
    for(int k = l2g[dep[x]] - 1; k >= 0; k--)
    {
        if(fa[x][k] != fa[y][k])
        x = fa[x][k], y = fa[y][k];
    }
    return fa[x][0];
}

RMQ

dfs遍历这棵树，每到达一个节点就记录下来（包括回溯），得到的序列称为欧拉序

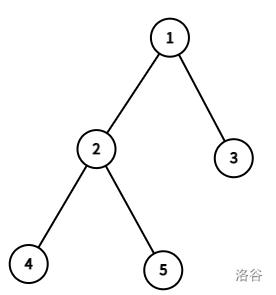
欧拉序

1	2	4	2	5	2	1	3	1

$id$ 记录节点第一次出现在欧拉序的编号

所以从 $u$ 到 $v$ 一定经过 $lca(u, v)$ 但不会经过 $lca(u, v)$ 的父亲，所以它们路径重 $id$ 最小的就是 $lca$

先dfs求出欧拉序再维护区间最值就行辣


int dfn[N << 1], dep[N << 1], T = 0;

void dfs(int u, int dp)
{
    dfn[++T] = u; pos[u] = T; dep[T] = dp;
    for(int i = head[u]; i; i = e[i].nxt)
    {
        dfs(e[i].to, dp + 1);
        dfn[++T] = u;
        dep[T] = dp;
    }
}

void initst()
{
  lg[0] = -1;
  for(int i = 1; i <= (N << 1); ++i) lg[i] = lg[i >> 1] + 1;
  for(int i = 1; i <= (N << 1) - 1; ++i) st[0][i] = dfn[i];
  for(int i = 1; i <= lg[(N << 1) - 1]; ++i)
    for(int j = 1; j + (1 << i) - 1 <= ((N << 1) - 1); j++)
        st[i][j] = dep[st[i - 1][j]] < dep[st[i - 1][j + (1 << i - 1)]]
                            ? st[i - 1][j]
                            : st[i - 1][j + (1 << i - 1)];
}

树剖

重链剖分

按子树大小分成轻儿子和重儿子，通向重儿子的边构成重链，这样把树整成了线性结构

图片来自oi-wiki

两次dfs

int fa[MAXN], dep[MAXN], siz[MAXN], son[MAXN];
//  节点父亲    节点深度    子树大小     重儿子
int id[MAXN], top[MAXN], cnt;
//  节点新编号  链顶节点
void dfs1(int u, int dad)
{
    siz[u] = 1; fa[u] = dad; dep[u] = dep[dad]+1;
	for(int i = head[u]; i; i = e[i].nxt)
    {
		int v = e[i].to; if(v == dad) continue;
        dfs(v, u);
        siz[u] += siz[v];
        if(siz[v] > siz[son[u]]) son[u] = v;
    }
}
void dfs2(int u, int tup)
{
    top[u] = tup; id[u] = ++cnt;
	if(son[u]) dfs2(son[u], tup);
    for(int i = head[u]; i; i = e[i].to)
    {
        int v = e[i].to;
        if(v == son[u] || v == fa[u]) continue;
        dfs2(v, v);
	}
}

LCA

树剖求出 $dep$ 和 $top$

对于 $u$ 和 $v$ ，如果他们在一条链上，那么它们重深度小的那个就是 $lca$

如果不在一条链上，那就把所在链的链顶深度深的向上跳，直到在一条链上

int lca(int u, int v)
{
    while(top[u] != top[v])
    {
		if(dep[top[u]] > dep[top[v]]) u = fa[top[u]];
        else v = fa[top[v]];
    }
    return dep[u] < dep[v] ? u : v;
}

P3384

树剖之后线段树维护，区间修改，区间求和

P2146