某不知名的 AHU 算法 和 树哈希
树同构问题
定义
有根树同构
对于两颗有根树 T1(V1,E1,r1) 和 T2(V2,E2,r2) 存在一个双射 φ:V1→V2 ,使得
∀u,v∈V1,(u,v)∈E1⟺(φ(u),φ(v))∈E2
且 φ(r1)=r2 成立,那么称有根树 T1 和 T2 同构。
无根树同构
对于两颗无根树 T1(V1,E1) 和 T2(V2,E2) 存在一个双射 φ:V1→V2 ,使得
∀u,v∈V1,(u,v)∈E1⟺(φ(u),φ(v))∈E2
那么称有根树 T1 和 T2 同构。
映射指两个元素的集之间元素相互对映的关系
设 f 是从集合 A 到集合 b 的映射,若 f(A)=B ,即 B 中任一元素 b 都是 A 中某元素的像,则称 f 为 A 到 B 上的满射;
若对 A 中任意两个不同元素 a1=a2,它们的像 f1=f2,则称 f 为 A 到 B 的单射;
若映射 f 既是单射,又是满射,那么称 f 为 A 到 B 的双射
我看不懂 😅😅😅 但是无关紧要
如果把 T1 上的节点重新标号使得 T1 与 T2 完全相同,那么两树同构
还有就是有根树同构,无根树同构
有根树同构显然更简单,考虑无根树转换成有根树同构,没有根我们就整一个根
看到从树上取出一个点来,考虑找树的重心
我们知道一棵树可能有一个或两个重心,所以分为这几种情况
AHU算法
前置:括号序
把一棵树用括号表示,每棵子树用一对括号括起来
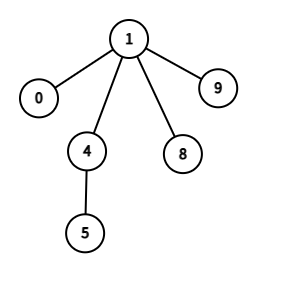
这颗树的括号序就是( () (()) () ())
标上号就是(1 (0) (4(5)) (8) (9))
所以一颗有根树存在一个唯一的括号序,而且这个括号序可以看成由他的字数的括号序拼接而来的,所以我们改变一下子树拼接的顺序,得到的新括号序对应的树与原树同构
递归求括号序时,把子树的括号序排个序再拼接,比较这样得到的括号序就行了
O(nlogn)
用这种方式需要比较两个字符串,而且当树是一条链时字符串会很长,最坏时间复杂度 O(n2)
考虑把括号序换成数值,对于一个节点,它的括号序只与他的儿子节点,也就是它的深度+1的节点有关,所以可以把树分层,然后用节点在它所在的层的排名代替括号,这样之后,每个节点的括号序变成了一个大小是节点字数大小的数组,对数组进行比较就行辣
算法流程
- 找重心,重心数量不同 return false
- DFS处理出节点深度,把深度相同的节点放到一个数组中
- 从小到大枚举深度,合并儿子括号序,排序,处理当前括号序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| void AHU()
{
for(int i = n-1; i >= 0; i--)
{
for(int j = 0; j < lv[i].size(); j++)
{
int v = lv[i+1][j];
f[fa[v]].push_back(dis[v]);
}
sort(lv[i].begin(), lv[i].end(), cmp);
int cnt = 0;
for(int j = 0; j < lv[i].size(); j++)
{
if(g[lv[i][j]] != g[lv[i][j - 1]])
cnt++;
dis[lv[i][j]] = cnt;
}
}
}
if(rt1.size() != rt2.size()) {printf("NO"); return 0;}
fa[rt1[0]] = 0; fa[rt2[0]] = 0;
dfs(rt1[0]); dfs(rt2[0]);
AHU();
if(g[rt1[0]] == g[rt2[0]]) {printf("YES"); return 0;}
if(rt2.size() == 1) {printf("NO"); retuen 0;}
fa[rt[2]] = 0; dfs(rt2[1]);
AHU();
printf(g[rt1[0]] == g[rt2[0]] ? "YES" : "NO");
|
树哈希
把树映射成一个哈希值,主要有三种方法
方法一
fu=sizeu×∑fson(u,i)×seedi−1
fu 表示 u 为根的子树的 hash 值
size 是以 u 为根的子树大小
son(u,i) 表示 u 的儿子们按 f 排序后第 i 个儿子
seed 是一个大质数
方法二
fu=⨁fson(u,i)×seed+sizeson(u,i)
son(u,i) 表示儿子节点(不排序)
⨁ 疑惑和
因为是异或,当存在多棵本质相同的子树时,这种子树出现次数1,3,5…时无法区分
方法三
fu=1+∑fson(u,i)×prime(sizeson(u,i))
prime(i) 第 i 个质数
使用这种方法需要先判定一下子树大小
我们求出的是子树的 hash 值,也就是说当选取的根对劲时两棵树才会判为同构
一种方法是暴力枚举以每个节点为根时的 hash
另一种方法是找重心,以重心为根进行 hash
平常使用也可以找重心来减少冲突
比如树是一条链,计算 hash 值时发现乘以 seed 的次数会很少








